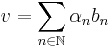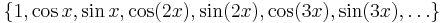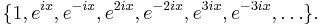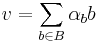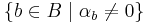Schauder basis

In mathematics, a Schauder basis or countable basis is similar to the usual (Hamel) basis of a vector space; the difference is that Hamel bases use linear combinations that are finite sums, while for Schauder bases they may be infinite sums. This makes Schauder bases more suitable for the analysis of infinite-dimensional topological vector spaces including Banach spaces.

Schauder bases were described by Juliusz Schauder in 1927,^[1]^[2] although such bases were discussed earlier. For example, the Haar basis was given in 1909, and Faber (1910) discussed a basis for continuous functions on an interval, sometimes called a Faber–Schauder system.

1 Definition
2 Examples and properties
- 2.1 Basis problem
3 Relation to Fourier series
4 Unconditionality
5 Related concepts
6 See also
7 Notes
8 References

Definition

Let V denote a Banach space over the field F. A Schauder basis is a sequence (b_n) of elements of V such that for every element v ∈ V there exists a unique sequence (α_n) of elements in F so that

$v = \sum_{n \in \N} \alpha_n b_n \,$

where the convergence is understood with respect to the norm topology. Schauder bases can also be defined analogously in a general topological vector space.

As opposed to a Hamel basis, the elements of the basis must be ordered since the series may not converge unconditionally.

Examples and properties

The standard bases of c₀ and l_p for 1 ≤ p < ∞ are Schauder bases.

Every orthonormal basis in a separable Hilbert space is a Schauder basis.

The Haar system is an example of a basis for L^p(0, 1) with 1 ≤ p < ∞. Another example is the trigonometric system defined below.

The Banach space C([0, 1]) of continuous functions on the interval [0, 1], with the supremum norm, admits a Schauder basis.

A Banach space with a Schauder basis is necessarily separable, but the converse is false, as described below. Every Banach space with a Schauder basis has the approximation property.

Basis problem

A theorem of Mazur asserts that every infinite-dimensional Banach space has an infinite-dimensional subspace that has a Schauder basis. A question of Banach asked whether every separable Banach space has a Schauder basis; this was negatively answered by Per Enflo who constructed a separable Banach space without a Schauder basis.^[3]

Relation to Fourier series

Let (x_n) be the sequence (in the real case)

$\{ 1, \cos x, \sin x, \cos(2x), \sin(2x), \cos(3x), \sin(3x), \ldots \} \,$

or (in the complex case)

$\{ 1, e^{ix}, e^{-ix}, e^{2ix}, e^{-2ix}, e^{3ix}, e^{-3ix}, \ldots \} .$

The sequence (x_n) (called the trigonometric system) is a Schauder basis for the space L^p[0, 2π] for any p > 1. For p = 2, this is the content of the Riesz–Fischer theorem. However, the set (x_n) is not a Schauder basis for L¹[0, 2π]. This means that there are functions in L¹ whose Fourier series does not converge in the L¹ norm.

Unconditionality

A Schauder basis 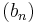$(b_n)$ is unconditional if whenever the series 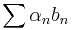$\sum \alpha_nb_n$ converges, it converges unconditionally. Unconditionality is an important property since it allows us to forget about the order of summation.

The standard bases of the sequence spaces 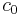$c_0$ and $l_p$ for 1 ≤ p < ∞, as well as every orthonormal basis in a Hilbert space, are unconditional.

The trigonometric system is not an unconditional basis in L^p, except for p = 2.

The Haar system is a unconditional basis in L^p for any 1 < p < ∞. Actually, the space L¹ has no unconditional basis.

A natural question is whether every infinite-dimensional Banach space has a infinite-dimensional subspace with an unconditional basis. This was solved negatively by Timothy Gowers and Bernard Maurey in 1992.

Related concepts

A Hamel basis is a subset B of a vector space V such that every element v ∈ V can uniquely be written as

$v = \sum_{b \in B} \alpha_b b \,$

with α_b ∈ F, with the extra condition that the set

$\{ b \in B \mid \alpha_b \neq 0 \} \,$

is finite. This property makes the Hamel basis unwieldy for infinite-dimensional Banach spaces; as a Hamel basis for an infinite-dimensional Banach space would be uncountable. (Every finite dimensional subspace of an infinite-dimensional Banach space X has empty interior, and is no-where dense in X. It then follows from the Baire category theorem that the a countable union of these finite-dimensional subspaces cannot serve as a basis^[4].)

A family of vectors is total if its linear span (the set of finite linear combinations) is dense in V. Every complete set of vectors is total, but the converse need not hold in an infinite-dimensional space.

If V is an inner product space, an orthogonal basis is a subset B such that its linear span is dense in V and elements in the basis are pairwise orthogonal.

Notes

This article incorporates material from Countable basis on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

^ J. Schauder, "Zur Theorie stetiger Abbildungen in Funktionalraumen", Mathematische Zeitschrift 26 (1927) pp. 47–65.
^ J. Schauder, "Eine Eigenschaft des Haarschen Orthogonalsystems, Mathematische Zeitschrift, 28 (1928) pp. 317–320.
^ Enflo, Per (July 1973). "A counterexample to the approximation problem in Banach spaces". Acta Mathematica 130 (1): 309–317. doi:10.1007/BF02392270.
^ N.L. Carothers, A short course on Banach space theory (2005), Cambridge University Press ISBN 0-521-60372-2

References

Heil, Christopher E. (1997). "A basis theory primer" (PDF). http://www.math.gatech.edu/~heil/papers/bases.pdf.
Schaefer, Helmut H. (1971). Topological vector spaces. GTM. 3. New York: Springer-Verlag. p. 114. ISBN 0-387-98726-6.
Gowers, W. Timothy; Maurey, Bernard (6 May 1992). "The unconditional basic sequence problem". arXiv:math/9205204.
Golubov, B.I. (2001), "Faber–Schauder system", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=f/f038020